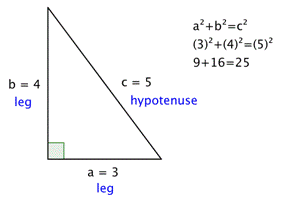
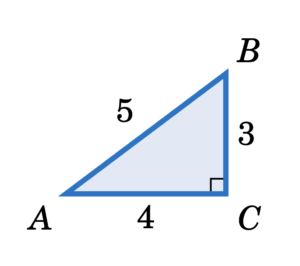
One of the two most famous is the 3–4–5 right triangle, where 3 2 4 2 = 5 2 In this situation, 3, 4, and 5 are a Pythagorean triple The other one is an isosceles triangle that has 2 angles measuring 45 degrees (45–45–90 triangle) Triangles that do not have an angle measuring 90° are called oblique triangles Answer 2 on a question 8 The ratio of the angles of a triangle is 345 Find the measure of each angle the answers to realanswersphcomTriangles When a triangle's sides are a Pythagorean Triple it is a right angled triangle See Pythagoras' Theorem for more details Example The Pythagorean Triple of 3, 4 and 5 makes a Right Angled Triangle Here are two more Pythagorean Triples 5, 12, 13 9, 40, 41 5 2 12 2 = 13 2 9 2
1
3 4 5 triangle angles
3 4 5 triangle angles-How to layout your foundation for building a shed, patio, garage or other structuresOther Combinations Yes, there are other




The Corresponding Angles Of The Two Triangles Add Up To Reflect The Download Scientific Diagram
Click here👆to get an answer to your question ️ Angles of a triangle are in the ratio 3 4 5 Find the angles Join / Login Question Angles of a triangle are in the ratio 3 4 5 Find the angles Medium Open in App Solution Verified by Toppr Angles are in the ratio of 3 4 5 Let the angles be 3 x, 4 x, 5 x ∴ 3 x 4 x 5 x = 1 8 0Sum of the angles of triangle are 1 8 0In the diagram, 4 is an exterior angle, and 1 and 2 are the two remote interior angles for this exterior angle A triangle with angles labeled 13 One side of the triangle extends forming exterior angle 4 that makes a linear pair with angle 3Additionally, the tool determined the last side length c = 1778 in Hanna Pamuła, PhD candidate Given angle and 2 sides Angle selection α α deg a in b in c in β deg γ deg Check out 16 similar triangle calculators 🔺 30 60
To get everything square you will now have to use the 345 triangle to provide a 90degree right angle The bigger you make this triangle the more accurate your marking out will be;Pythagorean Theorem and 3,4,5 Triangle How to work out the unknown sides of right angles triangle?To improve this 'Angles of a triangle Calculator', please fill in questionnaire Age Under years old years old level 30 years old level 40 years old level 50 years old level 60 years old level or over Occupation Elementary school/ Junior highschool student Highschool/ University/ Grad student A homemaker An office worker / A public employee Selfemployed people An engineer A
3 4 5 Right scalene Pythagorean triangle, area=6 Computed angles, perimeter, medians, heights, centroid, inradius and other properties of this triangle Triangle calculator the result Please enter what you know about the triangle Triangle You have entered side a, b, and c Right scalene Pythagorean triangle Sides a = 3 b = 4 c = 5 Area T = 6 Perimeter p = 12This downloadable 'Angles and Triangles' lesson pack for Year 5 has lesson plans, slideshow presentations and printable teaching resources #Lesson1ExploringAngles This Exloring Angles lesson begins by reminding children of the properties of angles, focusing initially on right angles Following this, the slideshow explains the differences between acute, obtuse and reflex anglesIn a right triangle, angle A measures ° The side opposite angle A is 10 centimeters long Approximately how long is the hypotenuse of the triangle?




Abc Has Three Angles C Is A Right Angle A And B Are Acute Angles We Can Make Ratios Related To The Acute Angles In Abc A Cb Ppt Download




Math Off The Grid 1 2 Triangles And Their Link To Pythagorean Triples
But the 345 triangle is the layman's substitute for the Pythagorean theorem The 345 triangle is the best way I know to determine with absolutely certainty that an angle is 90 degrees This rule says that if one side of a triangle measures 3 and the adjacent side measures 4, then the diagonal between those two points must measure 5 in Figure 549 The sine of π 3 equals the cosine of π 6 and vice versa This result should not be surprising because, as we see from Figure 549, the side opposite the angle of π 3 is also the side adjacent to π 6, so sin( π 3) and cos( π 6) are exactly the same ratio of the same two sides, √3s and 2sIf we substitute the numbers from a 345 triangle into this formula, we then have 9″ 16″ = 25″ Remembering the 345 Using triangle dimensions of 3, 4, and 5 is easy to remember and deploy There are no difficult equations to remember and the 345 method will always produce a perfect right angle very time



Two Squares With Sides Of Lengths 3 4 5 Placed At Right Angles To Each Other Clipart Etc



2
Learn How To Square A Roof With The Easy 3,4,5 Triangle Method Complete Step By Step Corrugated Metal Roofing Installation The 345 Method Is A Shortcut T3 2 4 2 = 5 2 Calculating this becomes 9 16 = 25 Yes, it is a Pythagorean Triple!It can be any common factor of these numbers For example, a 345 triangle



4 Setting Out Right Angles And Perpendicular Lines



Ks 3ks 4 Angles Skipton Girls High School
Exterior Angles of a Triangle When a side of a triangle is extended in a straight line, as in this diagram, the supplementary angle formed on the exterior of the triangle is called an exterior angle Note that the exterior angle and the adjacent interior angle form a linear pair of angles The two angles of the triangle that are not adjacent to the exterior angle are referred to as the remoteIt will even tell you if more than 1 triangle can be createdThe ratio 135 by doubling each number is the same as 2610 and the big one 10 is 10/(2610) = 10/18 of the total, so multiplying top and bottom by 10 gives 100/180, so the biggest angle is 100° since the sum of all angles must be 180°



Lesson Law Of Sines



Is Every Right Triangle A Rationed 3 4 5 Triangle Quora
Any triangle with sides of 3, 4 and 5 feet will have a 90 degree angle opposite the 5 foot side If a larger triangle is needed to increase accuracy of very large structures, any multiple of 345 could be used (such as a 6810 foot triangle or a foot triangle)And you have your "3,4,5" triangle with its right angle The Mathematics Behind It The Pythagoras Theorem says In a rightangled triangle, the square of a (a 2) plus the square of b (b 2) is equal to the square of c (c 2) a 2 b 2 = c 2 Let's check if it does work 3 2 4 2 = 5 2 Calculating this becomes 9 16 = 25 Yes, it works !3 4 5 Right scalene Pythagorean triangle, area=6 Computed angles, perimeter, medians, heights, centroid, inradius and other properties of this triangle 3 4 5 triangle Right scalene Pythagorean triangle Sides a = 3 b = 4 c = 5 Area T = 6 Perimeter p = 12 Semiperimeter s = 6 Angle ∠



Pythagorean Triples Ppt Download
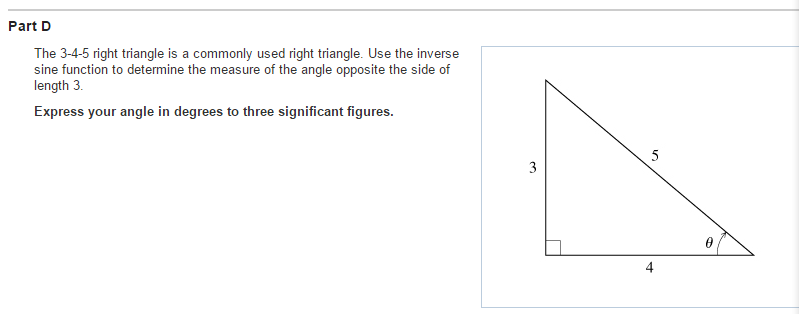



Solved Part Dthe 3 4 5 Right Triangle Is A Commonly Used Chegg Com
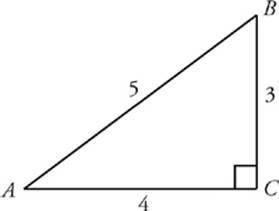
The Pythagorean 345 triangle is the only rightangle triangle whose sides are in an arithmetic progression 3 1 = 4, and 4 plus 1 = 5 The Kepler triangle is the only rightangle triangle whose side are in a geometric progression The square root of phi times Φ = 1 and 1 times Φ = Φ Although difficult to prove with certainty due to deterioration through the ages, this angleAnswer (1 of 4) I know that I will not be answering this completely But I have some interesting information to share you with 1 Triangle with sides 3 4 5 is a Pythagorean triangle 2 An angle ought to be 90° coz it is a Pythagorean triangle 3 Angle between sides 3 and 4 is 90°, between 4B = β = 531 3




3 4 5 Triangle Definition Math Open Reference




Special Right Triangles Video Lessons Examples And Solutions
The 5 12 13 triangle is an SSS special right triangle with the ratio between its side lengths as 5, 12, and 13 It is a common Pythagorean triple that is worth memorizing to save time when dealing with right triangles The other common SSS special right triangle is the 3 4 5 triangleThere are 4 types of triangle They all have 3 sides and are polygons 1 Equilateral 2 Isosceles Isosceles triangles have 2 equal sides and 2 equal angles 3 RightangledAngle 3 is either angle B or angle A, whichever is NOT entered Angle 3 and Angle C fields are NOT user modifiable Again, this right triangle calculator works



The Pythagorean Theorem
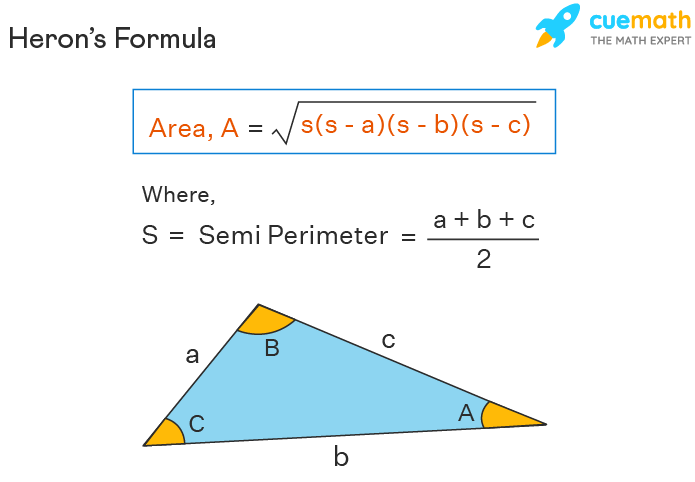



Area Of Triangle With 3 Sides Formula Definition Examples
Pythagorean Triples A right triangle where the sides are in the ratio of integers (Integers are whole numbers like 3, 12 etc) For example, the following are pythagorean triples There are infinitely many pythagorean triples There are 50 with a hypotenuse less than 100 alone Here are the first few 345 , 6810 , , , 815It could be 3 mm, 3 inches, 3 feet or 3 miles It doesn't matter theTriangles This section deals with 2D shapes and angles related to them It might be worth looking at the National 4 Angles section before continuing For any triangle, the three angles add up to



Info 345 Triangle Angles




Resources 3 4 5 Principle
No, because we can double the length of the sides of the 345 triangle and still have a rightangled triangle its sides will be 6810 and we can check that 10 2 = 6 2 8 2 Continuing this process by tripling 345 and quadrupling and so on we have an infinite number of Pythagorean triples 3 4 5 If a triangle has sides measuring 3, 4, and 5 feet (or any other unit), it must be a right triangle with a 90º angle between the short sides If you can "find" this triangle in your corner, you know the corner is square This is based on the Pythagorean Theorem from geometry A 2 B 2 = C 2 for a right triangle C is the longest side (hypotenuse) and A and B are the two shorter "legs" 345 The other two other modifiable values will be filled in, along with the angle 3 field In a triangle, all interior angles total to 180 degrees No two angles can total to 180 degrees or more Angle C is always 90 degrees;
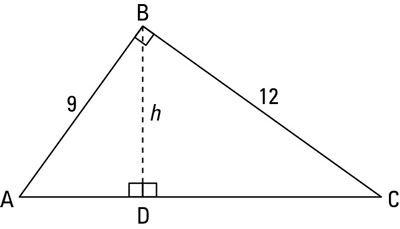



How To Solve Problems With The Altitude 0n Hypotenuse Theorem Dummies



Sides Vs Angles
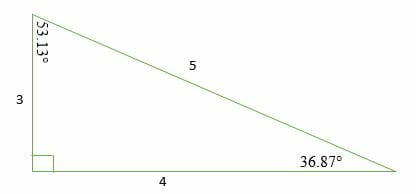
Example 3 In a triangle, If the second angle is 5° greater than the first angle and the third angle is 5° greater than second angle, find the three angles of the triangle Solution Let "x" be the first angle Then, the second angle = x 5 The third angle = x 5 5 = x 10 We know that, the sum of the three angles of a triangle = 180 ° x (x 5) (x 10) = 180 ° 3x 15 = 180A 345 right triangle has the three internal angles as 3687 °, 5313 °, and 90 ° Therefore, a 3 4 5 right triangle can be classified as a scalene triangle because all its three sides lengths and internal angles are different Remember that a 345 triangle does not mean that the ratios are exactly 3 4 5;A = α = 368 7 ° = 36°52'12″ = 064 4 rad Angle ∠
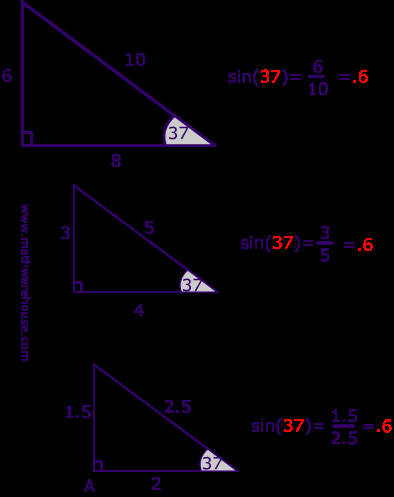



Pictures Of 3 4 5 Right Triangles Free Images That You Can Download And Use




Pythagorus Theorum Math Lesson 3 4 5 Triangle Youtube
Math Warehouse's popular online triangle calculator Enter any valid combination of sides/angles(3 sides, 2 sides and an angle or 2 angle and a 1 side) , and our calculator will do the rest!Using your tape measure (100m/330ft), You are best to use measurements of 30ft, 40ft and 50ft as your 345 First mark 30ft down the string line and place a peg34 centimeters 106 centimeters 275 centimeters 292 centimetersNone




Calameo Congruence Booklet
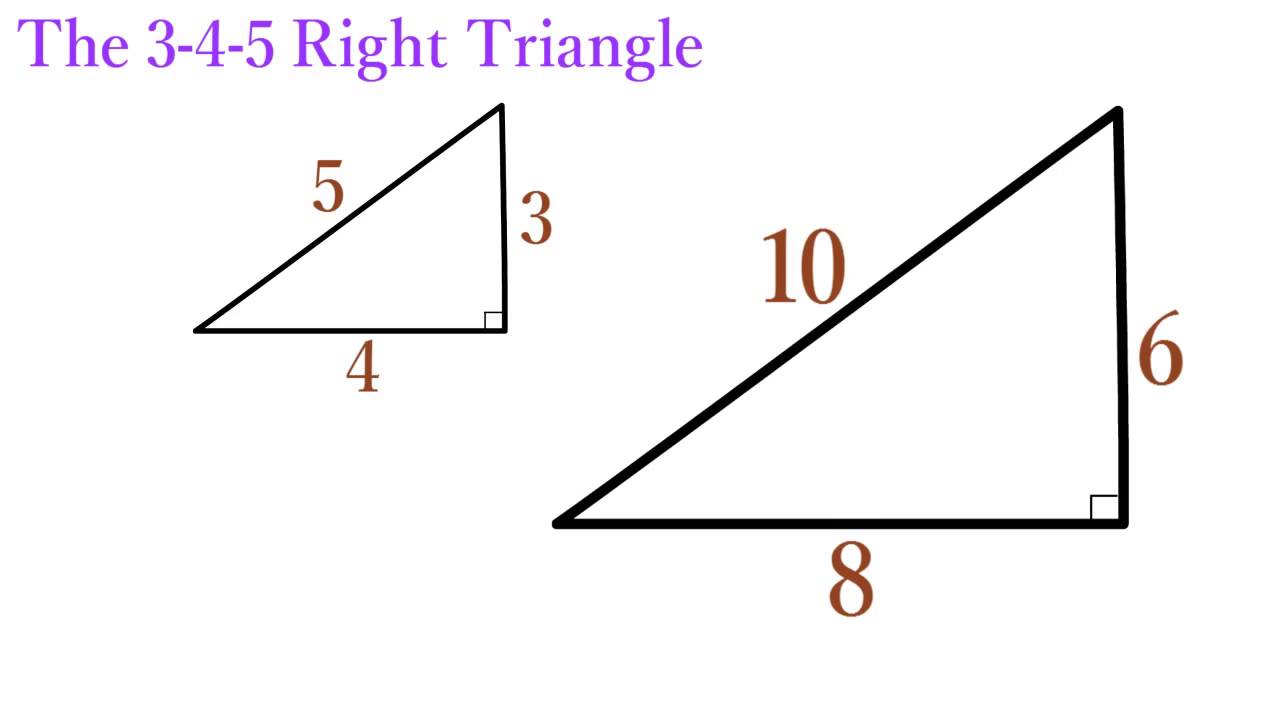



Lesson 12 The 3 4 5 Right Triangle Simplestep Learning Youtube
Characteristics of a 345 Right Triangle A right triangle is any triangle with one right angle of 90 oThere are several kinds of right triangles, but the 345 right triangle has special The triangle angle calculator finds the missing angles in triangle They are equal to the ones we calculated manually β = 5106°, γ = 94°;Show Stepbystep Solutions Pythagorean Triple 345 is an example of the Pythagorean Triple It is usually written as (3, 4, 5) In general, a Pythagorean triple consists of three positive integers such that a 2 b 2 = c 2 Other commonly used Pythagorean Triples are (5



What Is Triangle Definition Facts Example



Solution Hi I 39 M Having A Bit Of Trouble Do You Think You Could Help The Angles Of A Triangle Are In The Ratio 3 4 5 If The Shortest Side Has A Length Of
Any triangle with sides of 3, 4 and 5 feet will have a 90 degree angle opposite the 5 foot side If a larger triangle is needed to increase accuracy of very large structures, any multiple of 345 could be used (such as a 6810 foot triangle or a foot triangle)Although I asked for the determination of the largest angle of the 3 4 5 triangle (and this visual proof shows the other direction that the hypotenuse is a square on 5), I think the visual intuition is enough to go both directions, that showing a 3 4 rt triangle has hypotenuse 5 is enough (intuitively) to show the 3 4 angle of a 3 4 5 triangle is right Share Improve this answer FollowAnswer (1 of 4) We have to use the sine rule here If the triangle is ABC we have angles A, B and C and sides AB, BC and CA The rule says that AB/sin = BC/sin(A) = CA/sin(B) In a 345 triangle = ABBCCA we know CA = 5 is the hypotenuse and its opposite angle B is 90 degrees Sin(90 degr



Pythagoras Theorem Triangles And Trigonometry Mathigon




He Angles Of A Triangle Are In The Ratio 3 4 5 Find Each Of The Angles Brainly In
The 3 4 5 triangles are the only right triangles with edges in arithmetic progressionTriangles based on Pythagorean triples are Heronian, meaning they have integer area as well as integer sides The possible use of the 3 4 5 triangle in Ancient Egypt, with the supposed use of a knotted rope to lay out such a triangle, and the question whether Pythagoras' theorem wasThe angles of a triangle are in the ratio 135 What is the greatest angle? 345 triangles are used regularly in carpentry to ensure that angles are actually 90° We will use our knowledge of 345 triangles to check if some realworld angles




The Sine Function Selraybob



Apfstatic S3 Ap South 1 Amazonaws Com
You can find the angles of any shape of triangle using the cosine rule, if you know all three sides For a 345 triangle, you know one angle is right angle, so you can save time and use the definitions of sine and cosine instead of using the full cosine rule #5Interior Angles Because it is a right triangle one angle is obviously 90° The other two are approximately 3687° and 5313° An everyday example The 345 triangle is useful when you want to determine if an angle is a right angle For example, suppose you have a piece of carpet and wish to determine if one corner of it is 90° First measure along one edge 3 feet The measure along 41 Triangles and Angles (work)notebook A B D C 1 Theorem 43 Exterior Angle Theorem The measure of an exterior angle of a triangle is equal to the sum of the measures of the two nonadjacent interior angles m 1 = m A m C Corollary to the Triangle Sum Theorem The acute angles of a right triangle are complementary
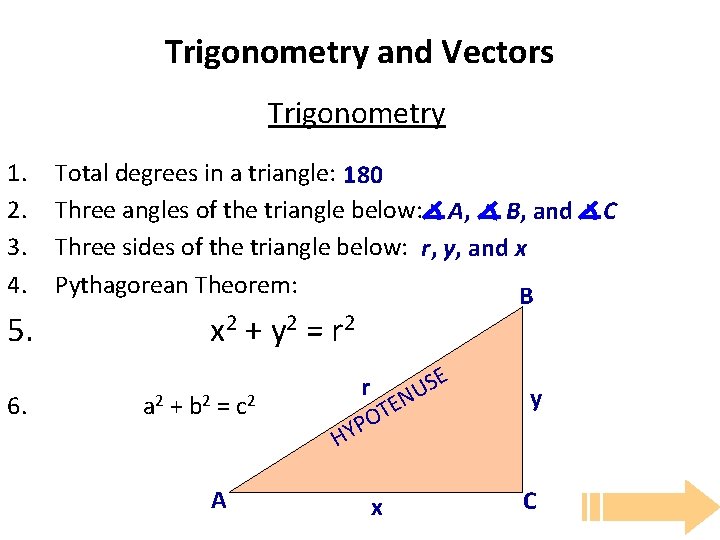



Trigonometry And Vectors Background Trigonometry 1 2 3
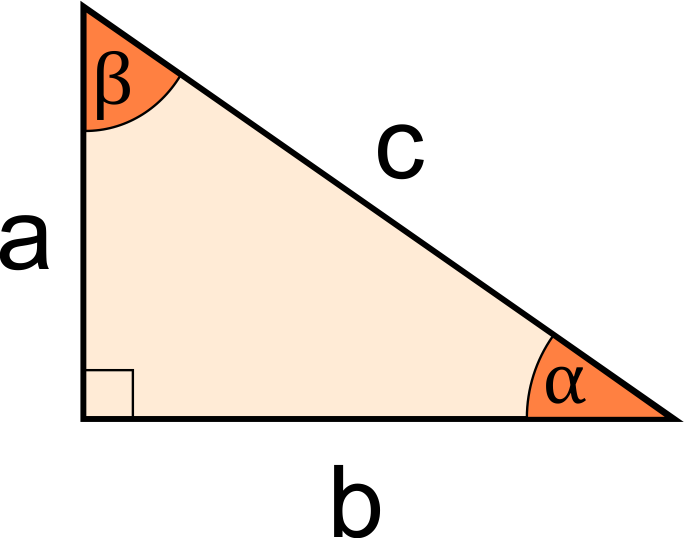



Right Triangle Calculator Find A B C And Angle
The 345 triangle is the best way I know to determine with absolutely certainty that an angle is 90 degrees This rule says that if one side of a triangle measures 3 and the adjacent side measures 4, then the diagonal between those two points must measure 5 in order for it to be a right triangle Confused yet?3 4 5 Triangle Angles The three internal angles in degrees are 3687, 5313, and 90 The three angles in radians are 064, 093, and 157 See the image below for the location of these angles How to Construct a 3 4 5 Triangle We can construct a 3 4 5 triangle by starting with a two lines that meet at a right angle Make the vertical line about 3/4 as long as the horizontal line ThenRatio in angles of a triangle is 3 5 7 But sum of angles of a triangle = 180° Sum of ratios = 3 5 7 = 15 First angle = \frac{180^{\circ}}{15}\times3=36^{\circ} Second angle = \frac{180^{\circ}}{15}\times5=60^{\circ} Third angle = \frac{180^{\circ}}{15}\times7=84^{\circ} Angle of the triangle are 36° , 60° and 84° "Hello, welcome to lido homework today We're



3 1 Trigonometric Functions Of An Acute Angle Precalculus




Triangle Wikipedia
Since these sides are in the ratio 3 to 4 and angle C is 90) the triangle is a 345 triangle Therefore, side AB represents the 5unit side of the triangle The ratio 30 to 40 to 50 is equivalent to 345, and thus side AB is 50 units long Practice problems Without reference to tables or to the rule of Pythagoras, solve the following problems 1 An observer is at the top of a 30foot



1



1



Getting Square With The 3 4 5 Triangle




Trigonometry Non Right Angled Triangles Mr Mathematics Com
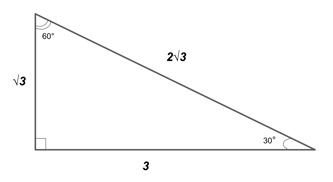



The Easy Guide To The 30 60 90 Triangle
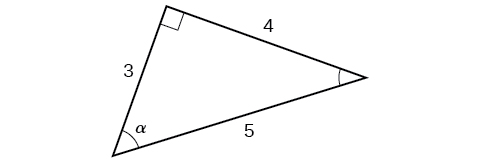



Right Triangle Trigonometry Algebra And Trigonometry



Laying Out An Accurate Archery Range Using Stem Principles




This Printable Triangle Has Two 45 Degree Angles And A 90 Degree Angle At Its Vertices Free To Download And Print Triangle Triangle Template Triangle Ruler
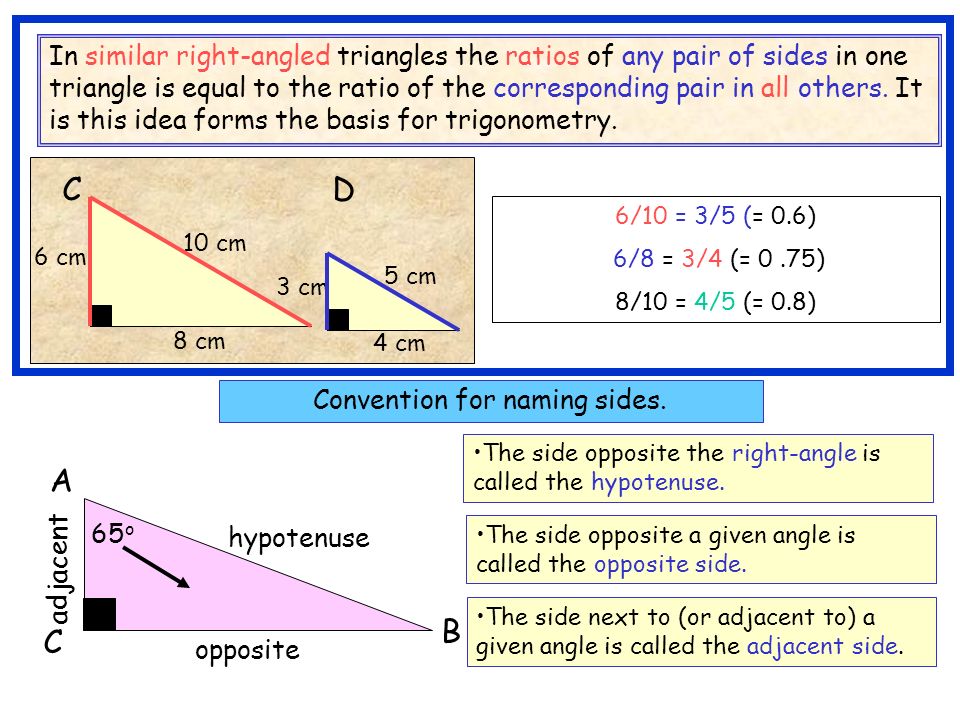



3 2 Powerpointmaths Com Quality Resources For The Mathematics Classroom Reduce Your Workload And Cut Down Planning Enjoy A New Teaching Experience Watch Ppt Download




3 4 5 Triangle Angles Sides How To Solve Full Lesson




Triangle Wikipedia
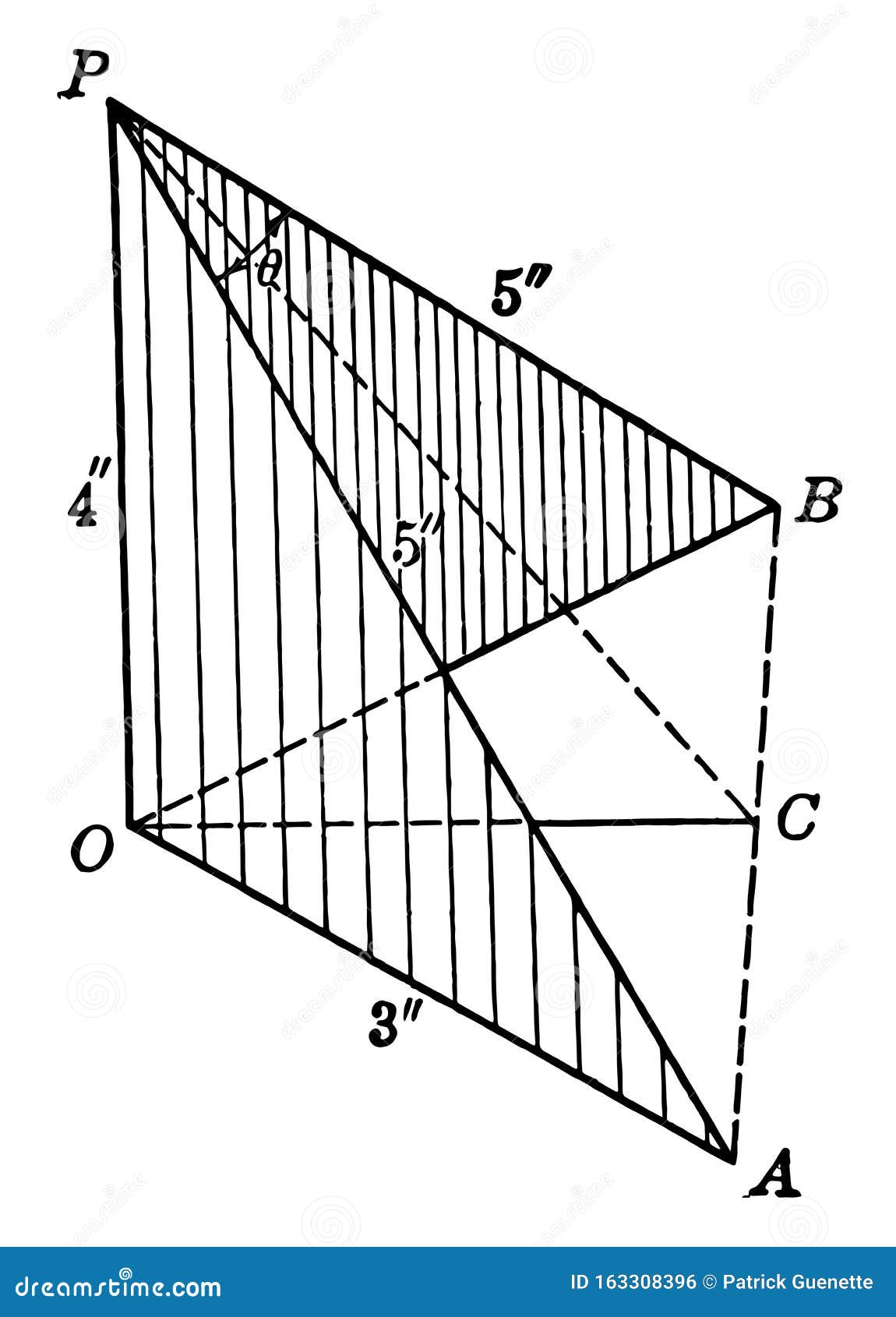



Two Squares With Sides Of Lengths 3 4 5 Placed At Right Angles To Each Other Vintage Illustration Stock Vector Illustration Of Angle Triangle
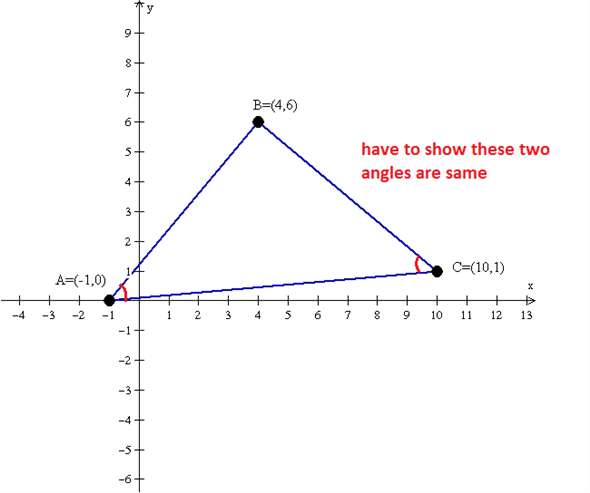



Solved Show By Means Of Angles That A 1 0 B 4 6 And Chegg Com




Catriona Agg What S The Angle




Triangle Congruence Section A Quiz
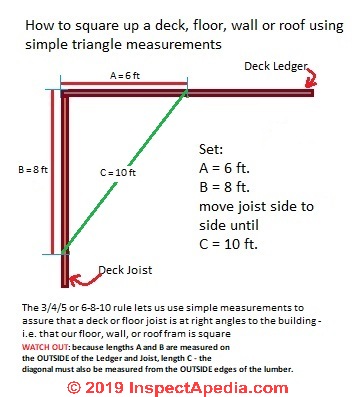



Use Triangles Simple Geometry To Aid Building Framing




3 4 5 Triangle Calculator Right Triangle Calculator Right Triangle Solver Special Triangles Right Triangle Pythagorean Triple Triangle




Triangle Wikipedia




3 4 5 Right Triangles Explanation Examples




Calculating Angles For A 5 12 13 Triangle Video Lesson Transcript Study Com




The Corresponding Angles Of The Two Triangles Add Up To Reflect The Download Scientific Diagram




3 4 5 Rule How To Make A Perfect Right Angle 3 4 5 Rule 3 4 5 Rule Guniya By Ce T Civil Engg Technology



What Is The Value Of Cos 53 Quora




3 4 5 Triangle Definition Math Open Reference




Calculating Angles For A 5 12 13 Triangle Video Lesson Transcript Study Com



3 4 5 Right Triangles Explanation Examples




If The Sides Of A Triangle Are In The Ratio 3 4 5 And The Perimeter Of The Triangle Is 72 Inches What Are The Lengths Of The Sides Study Com




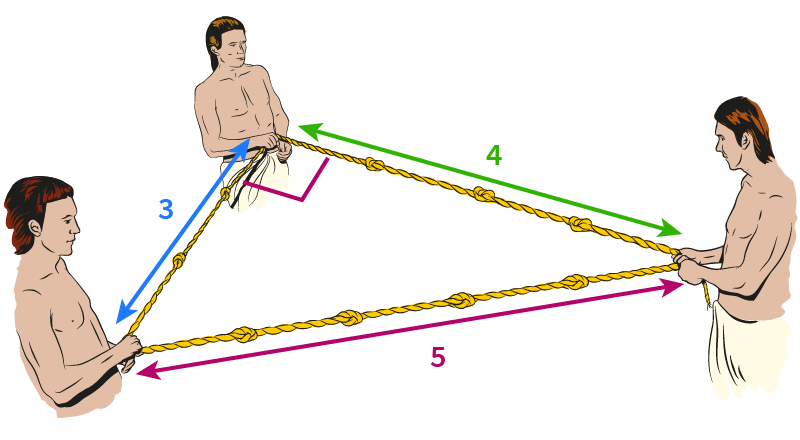
Khan Academy The Ancient Egyptians Had A Clever Way To Construct Right Angles To Start They Would Put 12 Knots Into A Long Rope Then They Would Pull The Rope Into



Triangle Calculator




Angles And Ratios Teaching Resources



In A Right Angle Triangle Tano 4 3 What Is The Value Of Sino Coso Quora




Pythagorean Triple 3 4 5 Pdf



1




3 4 5 Triangle Angles Sides How To Solve Full Lesson




If The Lengths Of The Sides Of A Triangle Are 3 5 7 Then Its Largest Angle Of The Triangle Is Youtube



Basic Trig Review Math Review Sat Physics Subject Test




Resources 3 4 5 Principle




Angles And Ratio Problems Foundation Crossover Teaching Resources




Hypotenuse Of A Triangle Calculator Formulas



Angles In 4 5 6 Triangle



Similarity And Congruence




Angles And Triangles Year 5 Maths By Planbee
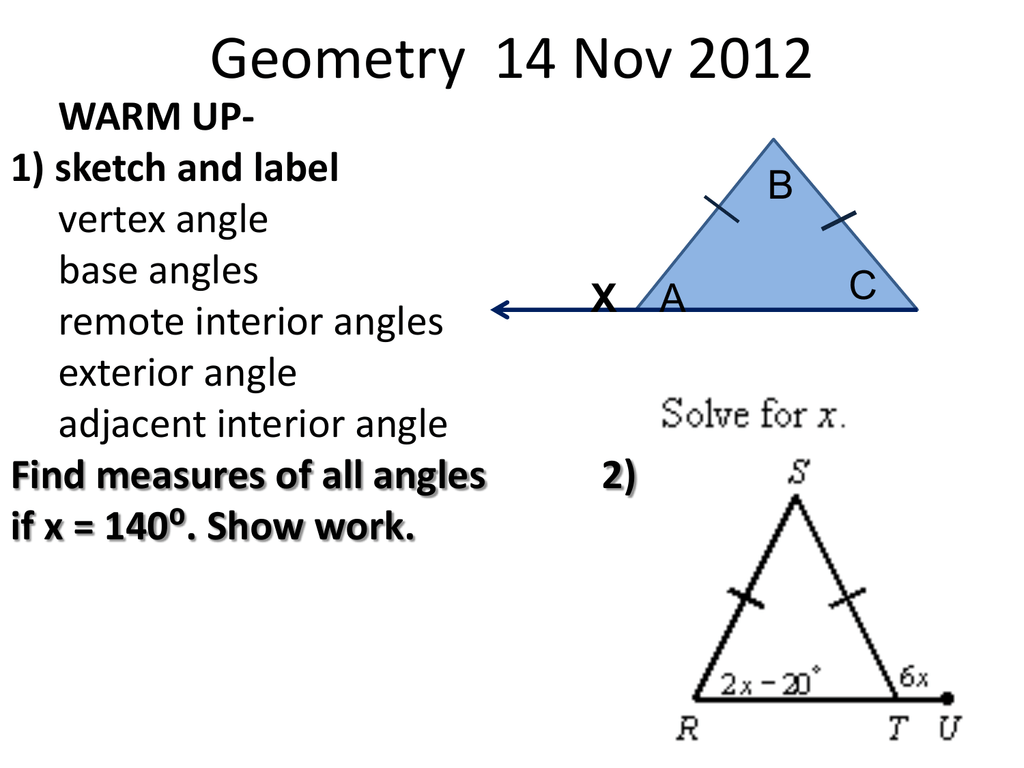



Geometry 14 15 Nov 12 4 3 4 5 Triangles Shope




Ratios In Right Triangles Ppt Video Online Download




Gmat Special Triangles Archives




Median Don Steward Mathematics Teaching Triangle Angles In A Ratio




Klaus Anton S Blog Why Is This Not A 3 4 5 Triangle




The Sine Function Selraybob



3 5 Triangle Angle Sum Pdf
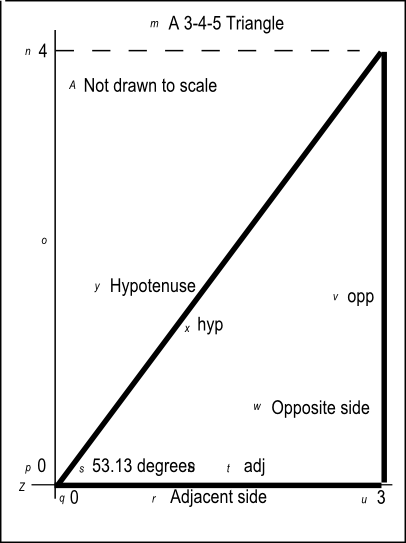



Sine Cosine And Tangent By Openstax Page 3 17 Jobilize
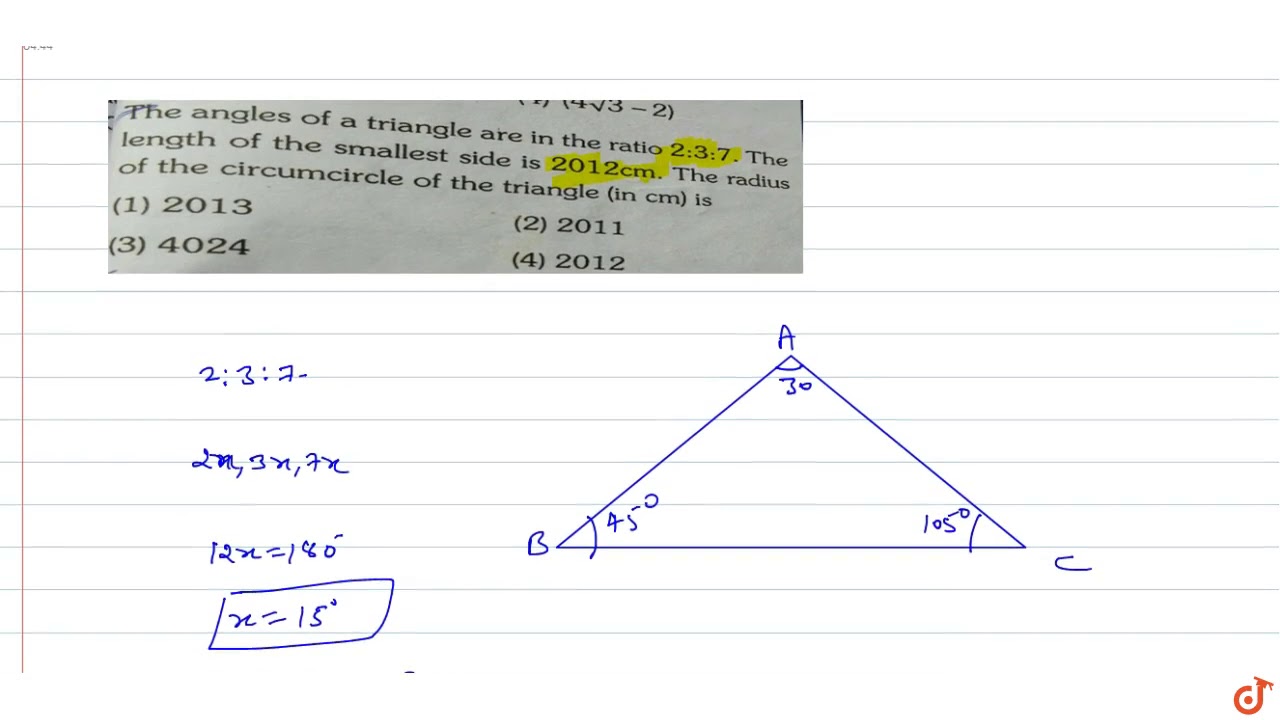



The Angle The Angles Of A Triangle Are In The Ratio 2 3 7 Thelength Of The Smallest Side Is Youtube




Comment Utiliser La Methode 3 4 5 Pour Construire Des Angles Droits




5 12 13 Triangle Angles Sides How To Solve Full Lesson
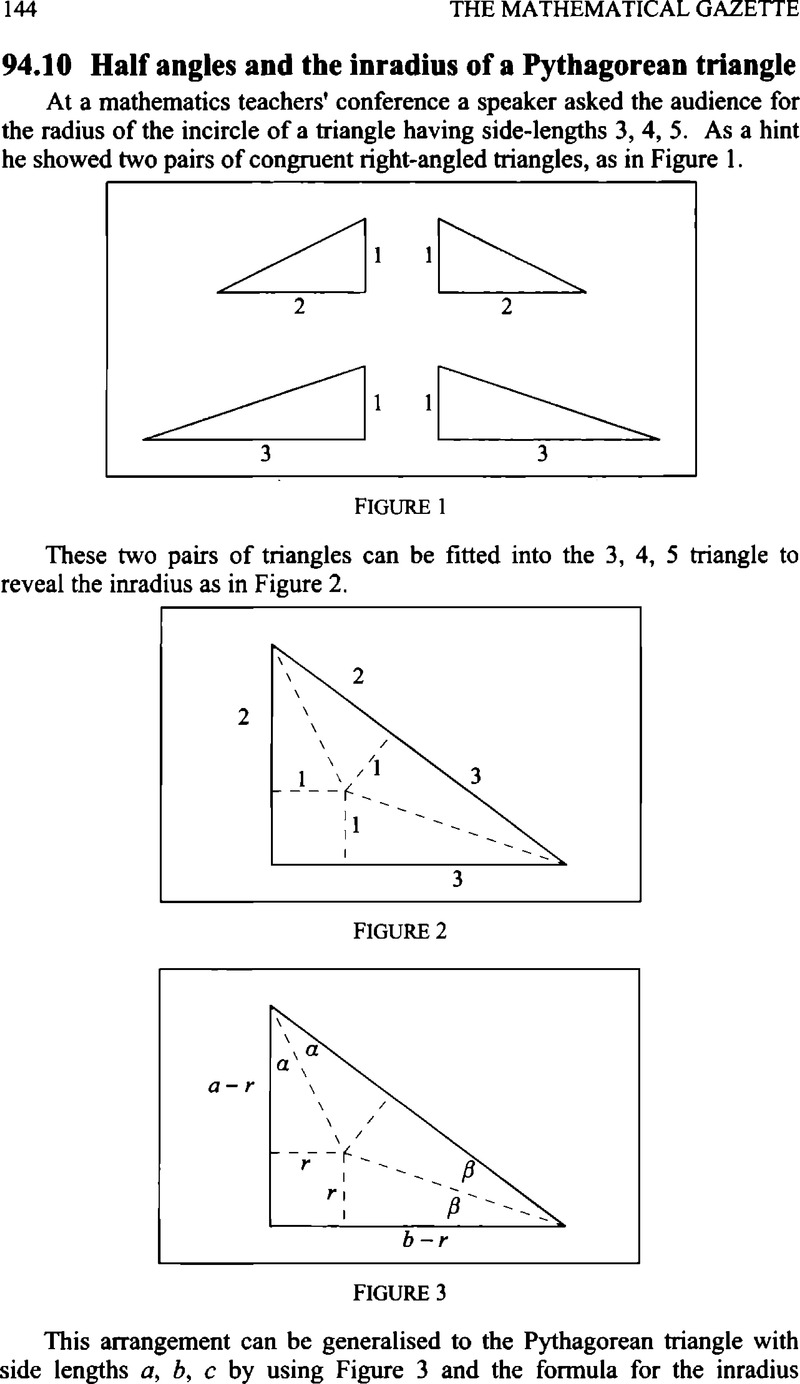



94 10 Half Angles And The Inradius Of A Pythagorean Triangle The Mathematical Gazette Cambridge Core
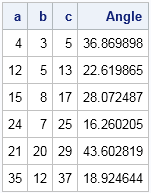



The Distribution Of Pythagorean Triples By Angle The Do Loop




Special Right Triangles 3 4 5 Triangle Study Com



Relations And Sizes Right Triangle Facts In Depth



The 3 4 5 Method For Squaring Corners Concord Carpenter



Trigonometric Functions Of An Acute Angle Opencurriculum




Pythagoras Theorem



A Triangle Contains 3 4 5 Points In Its Three Sides Excluding The Vertices How Many Triangles Can Be Drawn Quora
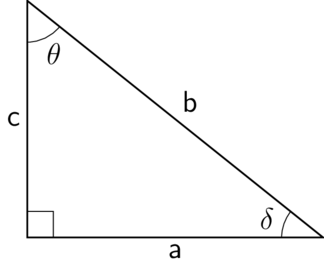



10 1 Trigonometric Ratios Trigonometry Siyavula




Basketball Math Lessons 1 Vince Carter And The Pythagorean Theorem 808s And Fastbreaks



4 Setting Out Right Angles And Perpendicular Lines



1




Manual Polygon Topo Builder
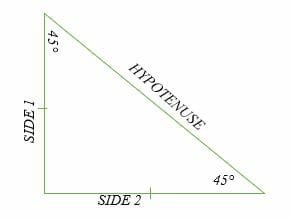



45 45 90 Triangle Explanation Examples




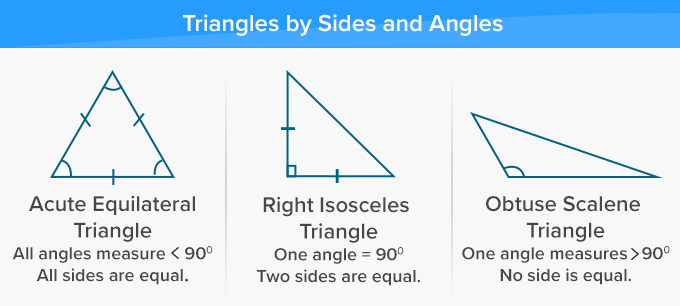
Acute And Obtuse Triangles Wikipedia




The Sides Of A Triangle Are In The Ratio 3 4 5 The Measure Of The Largest Angle Of The Triangle Youtube



Special Right Triangle 30 60 45 45 37 53 Elearning




The 3 4 5 Triangle Ssdd Problems



The Easy Guide To The 30 60 90 Triangle



0 件のコメント:
コメントを投稿